Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Étude du saut à la perche (gros problème de mécanique)

Posté par
Ennydra 07-12-14 à 23:31

Bonjour, bonsoir,

J'ai un problème qui se subdivise en 5 phases.

On doit étudier la discipline sportive du saut à la perche, décomposée en plusieurs phases.
Phase 1 : la course d'élan
Phase 2 : la flexion de la perche
Phase 3 : la détente de la perche
Phase 4 : la chute libre, phase ascendante
Phase 5 : la chute libre, phase descendante

On va commencer par la phase 1 (je ne sais pas si chacune des phases nécessite un topic différent ? il est dit que les phases peuvent être traitées indépendamment mais le tout regroupe UN exercice...) :

Le perchiste effectue une course d'élan de distance L en partant de l'arrêt. Cette course lui permet d'avoir une grande vitesse quand il plante sa perche et amorce son saut (phases qui seront abordées dans les parties suivantes). Le but de cette partie est de déterminer la vitesse du perchiste à la fin de sa course d'élan.

L'origine du système d'axes sera prise au point de départ de la course.
L'origine du temps sera prise au moment du départ de la course.

(a) En supposant que le perchiste est capable d'avoir une accélération constante de norme a0 déterminer l'équation horaire x(t) du perchiste lors de sa course.

(b) Exprimer la vitesse maximale vmax atteinte par le perchiste en fin de course en fonction de ao et L.

(c) Faites l'application numérique en prenant les valeurs suivantes : a0 = 1m/s² et L=40.5m.

Voilà ce que j'ai fait, mais j'ai du mal, je ne sais pas si mes réponses sont justes...

(a)
\vec{a}=\vec{cste}=a_0
a(t)=a_0 \\ v(t)=a_0t+v_0 sachant qu'à t=0, v0=0
x(t)=\frac{1}{2}a_0t^2+v_0t+x_0 sachant encore une fois qu'à t=0 on trouve x0=0

Donc l'équation horaire serait : x(t)=\frac{1}{2}a_0t^2=L

(b)
J'ai remplacé dans l'expression de v : v par vmax et t par tmax :
v_{max}=a_0t_{max} => t_{max}=\frac{v_{max}}{a_0}
Ce qui nous donne en injectant dans x :
x(t)=\frac{1}{2}a_0(\frac{v_{max}}{a_0})^2=\frac{1}{2}a_0\frac{v_{max}^2}{a_0^2}=\frac{a_0v_{max}^2}{2a_0^2}=L
L=\frac{a_0v_{max}^2}{2a_0^2} 2a_0^2L=a_0v_{max}^2 \sqrt\frac{2a_0^2L}{a_0} \sqrt{2a_0L}

(c)
AN
\sqrt{2a_0L} = \sqrt{2*1*40,5} = 9 m.s^{-1}.

J'ai fini pour cette première phase.
Pouvez-vous me dire si j'ai juste, faux, ou corriger les erreurs ?

Je vous remercie d'avance !

Bonne soirée ou journée à tous.

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 07-12-14 à 23:38

Petite coquille j'ai oublié le "vmax =" devant la première racine !

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 07:58

Bonjour,

Pour un même problème il ne faut créer qu'un seul topic.
__________

Je réponds à cette partie, même si lors de ton précédent topic tu n'as jamais répondu aux questions que je te posais pour terminer l'exercice...

Les origines des temps et de l'axe Ox, dirigé selon le mouvement, sont prises au départ :

a(t)\,=\,||\vec{a}||(t)\,=\,a_0

Intégrant, sachant que pour t = 0 s on a v(0) = 0 m.s-1

v(t)\,=\,a_0.t

Intégrant à nouveau et sachant que pour t = 0 on a x(0) = 0 m

x(t)\,=\,\dfrac{1}{2}.a_0.t^2

Notant t_{max} tel que x(t_{max})\,=\,L

t_{max}\,=\,\sqrt{\dfrac{2L}{a_0}}

Notant v_{max}\,=\,v(t_{max})

v_{max}\,=\,a_0.t_{max}\,=\,\sqrt{2.a_0.L}

Application numérique

v_{max}\,=\,\sqrt{2 \times 1 \times 40,5}\,=\,9\ \rm{m.s^{-1}}

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 14:22

Bonjour Coll et merci pour cette réponse complète !

"même si lors de ton précédent topic tu n'as jamais répondu aux questions que je te posais pour terminer l'exercice..."
---
Aie ! On avait dû me donner le corrigé et j'avais oublié de repasser pour prévenir Ce n'est pas très courtois, effectivement... D'autant plus que c'est grâce aux personnes comme vous, qui donnez de leur temps sur les forums que certains réussissent à s'en sortir (en tous cas pour ma part, les différents forums m'ont bien aidée !). A l'avenir, j'éviterai...

___

Ah oui, dans mon raisonnement j'ai dit que L était égale à x(t) avec t quelconque alors qu'effectivement, L est égale à x(t_max). Merci pour cette précision !

Passons maintenant à la phase 2 (je ne pense pas que l'on doive recréer un nouveau topic étant donné qu'on reprend même des données de la phase 1 !)... J'ai essayé de faire les premières questions mais je bloque réellement sur les dernières (et je ne suis même pas sûre d'avoir réussi les premières...)

Phase 2 : flexion de la perche

Une fois le perchiste au bout de sa course d'élan, il plante la perche dans un butoir et, en tenant très fermement l'autre extrémité de la perche, il la tord.

On peut modéliser cette phase comme la compression d'un ressort horizontal représentant la perche. Une extrémité du ressort est fixée au niveau du butoir, l'autre est mobile et une masse m représentant le perchiste y est accrochée. On modélise alors la flexion de la perche comme le mouvement d'une masse m accrochée au ressort, glissant sans frottements sur une surface horizontale.

Pour simplifier les calculs, vous allez prendre comme origine du système d'axes l'extrémité du ressort où est accrochée la masse m quand le ressort est à sa longueur à vide, et comme origine du temps le moment où le ressort commence à être comprimé.

A l'instant t=0, le ressort est à sa longueur à vide et la masse m a la vitesse v_{max} trouvée dans la partie précédente. Avec le nouveau système d'axes, la vitesse initiale de la masse m peut donc s'écrire : \vec{v_{max}}=v_{max}\vec{u_x}

(a) En prenant un ressort de raideur k, exprimez, pour un état de compression x donné, la force qui s'exerce sur la masse m. Faites un schéma faisant apparaître cette force \vec{F} pour un x>0 quelconque.

(b) En utilisant le principe fondamental de la dynamique, donnez l'équation différentielle du mouvement.

(c) Vérifiez que la fonction x(t)=Asin(t) est solution de l'équation du mouvement. Déduisez-en l'expression de .

(d) Donnez l'expression de A en fonction de k, m et v_{max}.

(e) Quelle est l'expression de la force maximale \vec{F_{max}} que le ressort exercice sur le perchiste ? Déduisez-en l'expression de la force maximale \vec{F_{p,max}} que le perchiste exerce sur le ressort lors de sa compression. Donnez la valeur numérique de la norme de cette force en utilisant les valeurs suivantes : v_{max}=9m.s^{-1}, m=81 kg et k=400 N.m^{-1}.

(f) Si vous comparez cette force à celle développée par un haltérophile, à quelle masse soulevée correspondrait-elle ?

___

Voici maintenant mes réponses :

(a) Sur le dessin \vec{T} est opposée à \vec{u_x}, donc \vec{T}=-kx\vec{u_x}= =-k(lo-l)>0.

Le dessin que j'ai reproduit se trouve en bas de page.

(b) Somme des forces extérieurs = m\vec{a}
\vec{P}+\vec{R}+\vec{T}=m\vec{a}
Sur [Ox) : \vec{-T}=m\vec{a}
T=ma donc -kx=mx'' donc x''+(k/m)*x=0

(c)
x = Asin(wt)
(on dérive)
x' = Awcos(wt)
(on re-dérive)
x'' = -Aw²sin(wt)=-w²x
Dans l'équation différentielle x^''+w²x=0 donc -w²x+w²x=0 est bien vérifiée (car k/m=w²);
Ainsi Asin(wt) est bien solution de l'équation.

L'expression de w est bien w=\sqrt\frac{k}{m}

(bon j'avoue que je connaissais déjà la formule de w donc je m'y suis sûrement mal pris)

(d) On a w²=k/m; vmax=Awcos(wtmax).
Donc v_{max}=A\sqrt\frac{k}{m}cos(\sqrt\frac{k}{m}t_{max}

Et c'est là où ça se corse... Faut-il isoler A ? Ma formule est-elle juste ? J'ai un gros doute...

Merci d'avance

Étude du saut à la perche (gros problème de mécanique)

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 14:52

"Dans l'équation différentielle x^''+w²x=0"
---
Le "^" est une faute de frappe.

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 16:32

a), b) et c) : d'accord.

d) À quel instant, dans ce mouvement de compression de la perche, la vitesse vaut-elle v_{max} ?

e) Que vaudra la vitesse à l'instant où la force sera maximale \vec{F}_{max} ?

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 18:59

Ah oui pour la (d) v=v_{max} lorsque t=0...

Donc sachant que w²=k/m et v_{max}=Awcos(w*0)=v_{max}=Aw*1=Aw...

Est-ce qu'on a :
v_{max}=Aw=A\sqrt\frac{k}{m} A=\sqrt{v_{max}\frac{m}{k}}.

C'est juste ?

Pour la (e), lorsque la force sera maximale, la vitesse sera nulle, non ?

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 08-12-14 à 20:59

D'accord avec v_{max}=A\sqrt\frac{k}{m}

Mais il faut recommencer la conclusion pour la valeur de A

Oui pour la e)

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 16:03

Alors moi je trouve v_{max}=A\sqrt\frac{k}{m} \frac{v_{max}}{\sqrt\frac{k}{m}}=A v_{max}\sqrt\frac{m}{k}=A...

C'est juste cette fois ?

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 16:16

Je tente de faire la (e) même si j'avoue avoir du mal D: !

Donc la force que le ressort exerce sur le perchiste, c'est bien la tension T=-kx. Lorsqu'elle est maximale, v=0 donc Awcos(wt)=0 !
La force (tension) est maximale lorsque la compression du ressort est maximale, c'est bien ça ?

Doit-t-on utiliser T(max)=-k(lo-l) ? Ça m'étonnerait puisque dans l'énoncé, on nous donne v_max comme données pour l'application numérique... Je me demande comment je dois m'y prendre...

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 16:29

(Excusez-moi pour ce troisième poste d'affilé !)

Il me semble que la "marche à suivre" serait de faire v(tmax)=0 soit Awcos(wtmax)=0. Ensuite, isoler tmax. Puis l'injecter dans x(tmax). Après grâce à la formule Tmax=-kx(tmax), on pourrait calculer Tmax !

Mais je doute que ce soit juste, donc j'attends la réponse

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 17:27

Oui A=v_{max}\sqrt\frac{m}{k}
________

Citation :
Lorsqu'elle est maximale, v = 0 donc A..cos(.t) = 0

Oui...
Quelle est la condition nécessaire et suffisante pour qu'un produit de facteurs soit nul ?

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 17:35

Qu'un des facteurs soit lui-même nul !

Dans notre cas ce serait soit l'amplitude A (impossible), soit w, soit cos(wt)...

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 17:43

Donc soit on a w=0 ET donc cos(0*t)=cos(0)=1...

Soit cos(wt)=0, ce qui implique (wt)=pi/2 ou -pi/2...

Mais même ainsi je ne vois pas comment déterminer la force exercée sur le ressort... Mon message de 16:29 est faux ?
Je bloque...

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 09-12-14 à 21:42

\vec{F}(t)\,=\,-\,k.x(t).\vec{u}\,=\,m.\vec{a}(t)

||\vec{F}|| sera donc maximale quand :
. x(t) sera maximal
. \vec{a}(t) sera maximal
. la vitesse sera nulle

et en effet, tout cela a lieu au même instant...

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 10-12-14 à 13:51

\vec{T}_{max}=-kx(t)\vec{u}=m\vec{a}(t)
Ce qui nous fait :
T=-k[Asin(wt)]=m[-w²(Asin(wt))].

Sachant que v(t)=Awcos(wt)=0, on a soit :
• w=0 qui implique cos(wt)=1 donc sin(wt)=0, ce qui n'est pas possible puisque lorsque T est maximale, x et a sont maximales.
• cos(wt)=0 donc wt=pi/2 ou -pi/2, donc sin(wt)=1 ou -1.
Donc x(t)=A ou x(t)=-A.
Et a(t)=-Aw² ou a(t)=Aw².

Ce qui ferait en injectant dans l'expression de T :
T=-kA=m[-w²(A)].
T=-kA+Amw²=A(k+mw²)=A(k+m\sqrt{k}{m}...

Mais encore une fois, vmax n'a pas été utilisé...

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 10-12-14 à 13:53

Oulah ça a buggé à la fin...

T=A(k+m\frac{k}{m})

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 10-12-14 à 15:00

Ben je pense que j'ai fait n'importe quoi...

Je n'y arrive vraiment pas...

Je reprends (erreurs de calculs au-dessus) :
J'ai trouvé que sin(wt)=1 ou -1... et donc x(t)=A ou -A.

Donc T=-kA=m(-w²A)
T=-kA+w²Am
T=A(-k+w²m)
T=A(-k+(k/m)m) [là si on simplifie on trouve 0 donc c'est pas possible)...
Et ensuite on remplacerait la valeur de A par celle trouvée à la question précédente soit A=vmax(racine(m/k)...

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 11-12-14 à 07:41

Je reprends ton message du 9 à 17 h 35

Est-ce que A peut s'annuler en fonction du temps ?
Est-ce que peut s'annuler en fonction du temps ?

Alors...

Quand cos(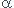) vaut 0, que vaut |sin()| ?

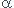Or on s'intéresse à cet ensemble de circonstances :

Citation :
||\vec{F}|| sera donc maximale quand :
. x(t) sera maximal
. \vec{a}(t) sera maximal
. la vitesse sera nulle


Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 11-12-14 à 12:25

Quand cos(a)=0, la valeur absolue de sin(a)=1 !

Ce qui nous ferait, x(t)=A (x maximale) et a(t)=-Aw² (a maximale).

En réinjectant dans F=-kx=ma :
F=kA=m(-Aw²)
F=kA-m(-Aw²)
F=A(k+mw²)
F=v_{max}\sqrt\frac{m}{k}(2k)
(j'ai remplacé A par la valeur trouvée à la question précédente, et w² par k/m)...

Y a sûrement un pb de signes...
Et je trouve une valeur de F anormalement élevée...

En tous cas merci pour cette grande patience...

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 11-12-14 à 13:11

Je ne comprends pas ta démonstration.

\vec{F}\,=\,-\,k.x.\vec{u}

\vec{F}_{max}\,=\,-\,k.A.\vec{u}

et donc

\vec{F}_{p,max}\,=\,k.A.\vec{u}

Il suffit, en effet, de remplacer, correctement, A par la valeur trouvée précédemment.

Quelle valeur trouves-tu pour ||\vec{F}_{p,max}|| ?

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 11-12-14 à 13:38

Aaaah !

En fait je m'amusais à faire depuis 2 jours :
\vec{F}_{max}=-kA.\vec{u}=m\vec{a} et à passer le m*a de l'autre côté de l'équation, en remplaçant a par sa valeur lorsque sin(wt)=1 (sachant que a=-Aw²sin(wt))...

Pourquoi se prendre autant la tête XD

Donc pour \vec{F}_{p,max}=k.A.\vec{u}, je trouve :
\vec{F}_{p,max}=k*v_{max}*\sqrt\frac{m}{k}

Donc Application Numérique :

\vec{F}_{p,max}=400*9*\sqrt\frac{81}{400}=1620 N.

Ça me paraît élevée !

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 11-12-14 à 17:12

C'est cela.

Mais l'écriture n'est pas simplifiée :

\vec{F}_{p,max}\,=\,k.v_{max}.\sqrt{\dfrac{m}{k}}\,=\,v_{max}.\sqrt{k.m}

Question f
Quelle masse, sur Terre, a un tel poids ?

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 12-12-14 à 18:20

Une masse de 162 kg a un tel poids !
Ça fait lourd pour un haltérophile je pense XD
Merci beaucoup pour cette précieuse aide et pour ce temps consacré ! Vraiment un grand MERCI !!!

Du coup je vais poster la phase 3, qui sera sûrement la dernière (je ne bloque pas trop sur les phases 4 et 5, qui représentent un exercice assez bateau de méca ^^)

Phase 3

Après avoir tordu la perche, le perchiste la redresse brutalement pour qu'elle se détende verticalement et l'élève. On modélise cette phase comme celle de la détente d'un ressort vertical sur lequel est posé une masse m (la masse du perchiste), sans chercher à étudier le passage de la position horizontale à la position verticale.

Dans cette partie, vous allez utiliser un repère avec un axe dirigé vers le haut. L'origine de l'axe est prise au niveau du sol (cf première figure en bas de page). L'origine du temps sera prise au moment où le ressort commence à se détendre.

Il est essentiel ici de ne pas oublier la contribution du poids.
On ne s'intéresse ici qu'au mouvement du perchiste selon l'axe vertical (son mouvement complet étant étudié lors de la dernière partie).

(a) En prenant un ressort de raideur k et de longueur à vide l_0, exprimez, dans ce nouveau repère, la force que le ressort exerce sur la masse m lorsqu'elle se trouve à une altitude zl_0. Faites un schéma en faisant apparaître cette force.

(b) Donnez l'expression du travail de la force élastique du ressort quand celui-ci passe d'un état comprimé (z=z_C) à un état où il est à sa longueur à vide (on a alors z=l_0).

(c) Donnez l'expression du travail de la force de pesanteur exercée sur la masse m entre z=z_C et z=l_0.

(d) En supposant que la vitesse initiale au moment de la détente est nulle, v_z(z_C)=0, donnez l'expression de la vitesse v_z(l_0)=0 de la masse m à la fin de la détente du ressort en fonction de k, m, g, l_0 et z_C ?

(e) Faites l'application numérique et vérifiez que v_z(l_0)=0m.s^{-1}. On donne les valeurs numériques suivantes : z_C=1,25m, k=400N.m^{-1}, l_0=5,25m et on prendra une approximation de la masse du perchiste à m=80kg pour effectuer le calcul.

Il manque donc de l'énergie à Sergueï Bubka qui veut atteindre son record du monde à plus de 6 m. Pour arriver à cette hauteur, le perchiste se donne en fait une énergie cinétique supplémentaire, E_C_{sup}, en donnant une impulsion verticale au moment où il quitte le sol (à ce moment son centre de gravité est en z=z_C, mais ses pieds touchent le sol).

(f) Donnez l'expression de E_C_{sup} nécessaire pour réaliser un saut de hauteur h=6,05m.

(g) Quelle est dans ce contexte la nouvelle vitesse v_Z'(l_0) du perchiste ? Donnez son expression littérale et faites l'application numérique.

_____

Pour la question (a), j'ai dessiné la tension T dirigée vers le haut (sur le premier dessin QUI NOUS EST DONNÉ AINSI). J'ai également fait un autre dessin, lorsque le ressort est à sa position d'équilibre (donc à la fin de la détente).

\vec{T}=-kx\vec{u_z}=-k(l_0-z_C)\vec{u_z} (on a bien l_0-z_C ?)

Pour la (b), j'ai fait :
W_{z_c->l_0}=\frac{1}{2}k(l_0^2-z_c^2)=\frac{1}{2}k(x^2)

Pour la (c) :
W_{z_c->l_0}=mg(z_c-l_0)

Pour la (d) :
Là j'ai pensé à faire Em_{z_C}=Em_{l_0} donc Ec_{z_C}+Epe_{z_C}=Ec_{l_0}+Epe_{l_0}, ce qui ferait (car l'énergie mécanique se conserve comme le système ne subit pas de frottements) :
\frac{1}{2}k(zc)²=\frac{1}{2}mv²(lo)+1/2k²(lo)...
Et là on en tire v(lo)...
Le pb c'est que dans ce cas, g n'aura pas été utilisé...
Et si j'utilise l'énergie potentielle de pesanteur, k ne sera pas utilisé...

Comment faire pour la question (d) ?

Étude du saut à la perche (gros problème de mécanique)

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 12-12-14 à 18:48

Je vais essayer d'être plus claire pour la question d...

Comme l'énergie mécanique se conserve, ça donne :
Em_{z_C}=Em_{l_0} donc
Ec_{z_C}+Epe_{z_C}=Ec_{l_0}+Epe_{l_0}

On sait que Ec_{z_C}=0 car l'énoncé nous dit que v_{z_C}=0...

Donc :
\frac{1}{2}kz_C^2=\frac{1}{2}kl_0^2+\frac{1}{2}mv_{l_0}^2

\frac{1}{2}kz_C^2-\frac{1}{2}kl_0^2=\frac{1}{2}mv_{l_0}^2

\frac{1}{2}k(z_C^2-l_0^2)=\frac{1}{2}mv_{l_0}^2

\frac{k(z_C^2-l_0^2)}{m}=v_{l_0}^2

\sqrt\frac{k(z_C^2-l_0^2)}{m}=v_{l_0}

Et dans ce cas, g n'aura pas été utilisé, alors que l'énoncé nous demande de trouver la vitesse également en fonction de g...

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 12-12-14 à 21:37

Bonsoir,

3.a)
Je ne comprends pas le signe "moins"
La force \vec{F} exercée par la perche (le ressort) sur la masse (le perchiste) a bien le sens du vecteur \vec{u}_z
Or k et (l0 - zC) sont des quantités positives.

3.b)
Non. Tu continues d'appliquer des "formules" sans chercher à les comprendre.
La question 3.b suit évidemment la question 3.a
Tu as l'expression de la force pour une valeur de z
Il faut en déduire le travail de cette force quand son point d'application varie de zC à l0

3.c)
Oui pour le travail du poids.

3.d)
Il suffit d'appliquer le théorème de l'énergie cinétique.

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 12-12-14 à 22:48

Oui le signe - n'a rien à faire puisque la tension est dans le même sens que le vecteur uz...

On a donc bien \vec{T}=k(l_0-z_c)\vec{u_z}

Le déplacement x (ou z) étant lo-zc...
Le travail de cette force est bien : 1/2*k*(lo²)-1/2*k*(zc)²=1/2*k(lo²-zc²)=k(lo-zc)²/2 ?
En tous cas, c'est comme ça qu'on l'a appris :/

Le théorème de l'énergie cinétique donnerait :
E_c=\dfrac{1}{2}mv_{l_0}-\dfrac{1}{2}mv_{z_C}=\dfrac{k(l_0-z_C)^2}{2}+mg(z_C-l_0)

La variation d'énergie cinétique étant égale à la somme des travaux des forces conservatives et non conservatives...
Avec l'énergie cinétique en z_C nulle, on retrouve l'expression de v_{l_0}. Mais avant de me lancer, j'essaye d'avoir la bonne expression du travail de la force élastique !

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 12-12-14 à 22:52

J'ai oublié les carrés dans l'expression des énergies cinétiques ^^

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 13-12-14 à 08:12



Citation :
1/2*k*(lo²)-1/2*k*(zc)²=1/2*k(lo²-zc²)=k(lo-zc)²/2


Il va falloir revoir le programme de quatrième...
a2 - b2 n'est pas égal à (a - b)2
____________

3.b)
La force exercée par le ressort quand son extrémité est à la hauteur z est \vec{F}\,=\,k(l_0\,-\,z).\vec{u}
Dans un déplacement dz.\vec{u} le travail élémentaire de cette force est dW tel que

dW\,=\,k(l_0\,-\,z).\vec{u} \cdot dz.\vec{u}\,=\,k(l_0\,-\,z).dz

Quand l'extrémité du ressort passe de z = zC à z = l0 le travail de la force fournie par le ressort est donc :

W\,=\,\int_{z_C}^{l_0}k(l_0\,-\,z).dz

Je pense que tu sauras calculer cette intégrale et retrouver W\,=\,\dfrac{1}{2}.k.(l_0\,-\,z_C)^2
mais cette fois d'une manière "mathématiquement correcte"...

Bien sûr il aurait été possible d'écrire que pour un raccourcissement de x l'énergie que peut restituer le ressort est W\,=\,\dfrac{1}{2}.k.x^2 et donc que W\,=\,\dfrac{1}{2}.k.(l_0\,-\,z_C)^2
__________

3.d)
Oui pour ton application du théorème de l'énergie cinétique. Mais ce n'est pas fini.
On te demande l'expression de v_z(l_0)

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 13-12-14 à 15:36

Oulah ah ben oui, x² ça fait pas (lo²-zc²) mais bien (lo-zc)²...
J'ai pas intérêt à faire ça le jour de l'exam...

J'ai enfin pu vérifier que la vitesse en v(lo)=0m/s :

E_c=\dfrac{1}{2}mv_{l_0}^2-0=\dfrac{1}{2}k(l_0-z_C)^2+mg(z_C-l_0)

Après plusieurs équations on retrouve finalement :

v_{l_0}=\sqrt{\dfrac{k(l_0-z_C)^2}{m}+2g(z_C-l_0)}

AN :
v_{l_0}=\sqrt{\dfrac{400(5,25-1,25)^2}{80}+2*10(1,25-5,25)}=\sqrt{80-80}=0m.s^{-1}

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 13-12-14 à 17:08

D'accord pour l'expression de v_{l_0} :

\boxed{ v_{l_0}=\sqrt{\dfrac{k(l_0-z_C)^2}{m}\,-\,2g(l_0-z_C)}}

À quelle condition cette vitesse est-elle nulle ?

Il faut :
\dfrac{k(l_0-z_C)^2}{m}\,=\,2g(l_0-z_C)
c'est-à-dire :
l_0-z_C\,=\,2.\dfrac{m.g}{k}

Il faut donc que le ressort soit raccourci d'une longueur double de celle qui résulterait d'une force égale au poids m.g
_________

Les valeurs données pour l'application numérique remplissent bien cette condition.

Avec une masse de 80 kg
et un poids de 800 N
le ressort de raideur 400 N.m-1
devrait se raccourcir de 800 / 400 = 2 m

Or le ressort est raccourci de 5,25 - 1,25 = 4 mètres, soit deux fois plus.

Posté par
Ennydrare : Étude du saut à la perche (gros problème de mécanique) 14-12-14 à 18:38

Re,
Merci beaucoup pour ces détails

Pour que le perchiste atteigne son record à une hauteur h=6,05 m, il faudrait en fait "remplacer" lo par h ? Le ressort se raccourcirait de 6,05 - 1,25 = 4,8 mètres.

Puis après ça, tenter de trouver l'énergie cinétique supplémentaire nécessaire ?

Posté par
Coll Moderateurre : Étude du saut à la perche (gros problème de mécanique) 14-12-14 à 18:49

Il ne me semble pas que ce soit des détails. Je me demande si tu comprends la logique du problème...
___________

Question 3.f
Quelle est l'énergie nécessaire pour atteindre 6,05 m ?

De quelle énergie dispose-t-il dans la perche ?
Quelle est donc l'énergie supplémentaire nécessaire ?


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !