Inscription / Connexion Nouveau Sujet
Energie libérée (transformations nucléaires)
Bonjour,
Je cherche à mieux comprendre comment on calcule l'énergie libérée (la physique-chimie n'étant pas ma spécialité pour le bac). Dans mon cours on me donne trois exemples d'exercices corrigés.
Je vous donne d'abord les formules et dans le post suivant je vous envoie les exos (et mes question)


| 1er exercice : Le bismuth 212
Le bismuth 212 est radiactif 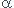 selon la réaction : selon la réaction :
21283Bi  20881Tl + 42He 20881Tl + 42He
Données : masse Bi 212 = 3,519422.10-25kg masse Tl 208 = 3,452865.10-25kg masse He 4 = 6,6456.10-27kg célérité2 = 9,00.1016 charge de l'électron q = -1,60.10-19C On m'a demandé de calculer l'énergie libérée par cette réaction. En accord avec la correction j'ai trouvé : La perte de masse au cours de cette réaction vaut :  m = mBi - mTl - mHe m = mBi - mTl - mHe
 m = 1,01.10-29kg. m = 1,01.10-29kg.
Cela signifie que la différence entre l'énergie de masse du noyau père et l'énergie de masse du noyau fils et de la particule émise vaut : E =  m.c2 (donné par la propriété 1) m.c2 (donné par la propriété 1)
E = 9,09.10-13J Que l'on convertit en MeV soit : L'énergie libérée est donc de 5,7 MeV. |
Pourquoi avoir donné la charge de l'électron q pour ne pas l'avoir utiliser ? Si j'utilise cette donné comment je résous ce même exercice ?
J'ai essayé le même exercice en y intégrant la charge de l'électron q. Ce qui m'a donné :
 m =
m =  masse des produits -
masse des produits -  masse des réactifs
masse des réactifs
 m = 3,519321.10-25 - 3,519422.10-25
m = 3,519321.10-25 - 3,519422.10-25
 m = -1,01.10-29kg.
m = -1,01.10-29kg.
 m = -9,09.10-13J
m = -9,09.10-13J
Ensuite j'ai appliqué la formule Ecinétique = q.u soit u = Ec/q
u = 5,68125.106 J/C
sauf que là je ne sais pas comment terminer (je veux dire comment convertir en MeV).
Pourriez-vous m'aider ? ou si la manière dont j'ai intégré la charge de l'électron est fausse, pourriez-vous m'expliquer comment l'intégrer... pour trouver finalement l'énergie libérée ?
Excuse moi, mais ce soir, je ne serai pas dispo.
Si personne ne t'aide, je répondrai à tes questions demain matin GMT+2
PS : J'attends toujours que tu me résumes le sujet sur l'uranium et as tu continué le sujet de fusion ?
Dans mon exercice du Bismuth, il semble que l'énergie libérée se calcule grâce à la formule :
E =  m.c2 (où
m.c2 (où  m = masse des réactifs - masse des produits).
m = masse des réactifs - masse des produits).
Dans un autre exercice "réacteur nucléaire utilisé pour la propulsion" dont la réaction est 23592U + 10n 9438Sr + 14054Xe + 210n. Ils ont utilisé exactement la même formule sauf que les masses étaient données en u, puis le défaut de masse obtenu a été converti en kg.
9438Sr + 14054Xe + 210n. Ils ont utilisé exactement la même formule sauf que les masses étaient données en u, puis le défaut de masse obtenu a été converti en kg.
Energie libérée par chaque fission : E =  m.c2
m.c2
GMT+2 ? il est 20h29 + 2 chez toi ?
je préférerai d'abord comprendre comment on calcule l'énergie libérée (il me semble qu'il me faut d'abord comprendre entièrement cette notion, qu'il ne me reste aucun doute avant de pouvoir continuer) je pourrai ainsi revoir mon topic "noyau d'uranium 235" et comprendrai peut-être mieux pour "l'énergie solaire"....
Quelqu'un pourrait-il mieux m'expliquer quand je dois utiliser la propriété et quand je dois utiliser la propriété 2, s'il vous plaît ?
Je refais ton exercice du début (celui du message du 12-08-10 à 19:48) par la méthode de la différence des énergies de liaison.
----------------------
Calcul par la différence des énergies de liaison.
Pour cela on a besoin aussi de la masse d'un proton et de la masse d'un neutron, les voici:
masse d'un proton : 1,6726.10^-27 kg
masse d'un neutron : 1,6749.10^-27 kg
Calcul de l' énergie de liaison d'un noyau de Bi(83,213):
83 protons : masse = 83 * 1,6726.10^-27 = 1,38826.10^-25 kg
(212-83) = 129 neutrons: masse = 129 * 1,6749.10^-27 = 2,160621.10^-25 kg
masse totale des protons et neutrons d'un noyau de Bi(83,213) = 1,38826.10^-25 + 2,160621.10^-25 = 3,548881.10^-25 kg
Energie de liaison d'un noyau de Bi(83,213) = (3,548881.10^-25 - 3,519422.10^-25) * c² = 2,9459.10*-27 * (3.10^8)² = 2,65131.10^-10 J
---
Calcul de l' énergie de liaison d'un noyau de Tl(81,208):
81 protons : masse = 81 * 1,6726.10^-27 = 1,354806.10^-25 kg
(208-81) = 127 neutrons: masse = 127 * 1,6749.10^-27 = 2,127123.10^-25 kg
masse totale des protons et neutrons d'un noyau de Tl(81,208) = 1,354806.10^-25 + 2,127123.10^-25 = 3,481929.10^-25 kg
Energie de liaison d'un noyau de Tl(81,208) = (3,452865.10^-25 - 3,481929.10^-25) * c² = 2,9064.10*-27 * (3.10^8)² = 2,61576.10^-10 J
---
Calcul de l' énergie de liaison d'un noyau de He(4,2):
2 protons : masse = 2 * 1,6726.10^-27 = 3,3452.10^-27 kg
(4-2) = 2 neutrons: masse = 2 * 1,6749.10^-27 = 3,3498.10^-27 kg
masse totale des protons et neutrons d'un noyau de He(4,2) = 3,3452.10^-27 + 3,3498.10^-27 = 6,695.10^-27 kg
Energie de liaison d'un noyau de He(4,2) = (6,695.10^-27 - 6,6456.10^-27)*c² = 0,0494.10^-27 * (3.10^8)² = 4,446.10^-12 J
---
Energie de liaison pour le membre de gauche de la réaction : 2,65131.10^-10 J
Energie de liaison pour le membre de droite de la réaction : 2,61576.10^-10 + 4,446.10^-12 = 2,66022.10^-10 J
Energie libérée par la réaction = 2,66022.10^-10 - 2,65131.10^-10 = 8,91.10^-13 J
La reponse est un rien différente que par la méthode du défaut de masse, cela est du à la pàrécison avec laquelle on avait les masses d'un proton et d'un neutron (moins de décimales que les autres données).
Si on utilise suffisamment de décimales, les 2 méthodes donnent la même réponse.
------------------
On peut donc utiliser n'importe laquelle des 2 méthodes, les résultats sont les mêmes.
Suivant les données qu'on possède, on utilise l'une ou l'autre.

Je vous remercie J-P !
et pour la donnée de la charge d'un électron q... elle ne sert donc à rien pour calculer l'énergie libérée ou autre calcul... ?
 Ah, d'accord ! J'ai compris. Cette fois-ci je crois bien que c'est bon.
Ah, d'accord ! J'ai compris. Cette fois-ci je crois bien que c'est bon.
Je vous remercie pour votre aide ! 

 ?
?

