Inscription / Connexion Nouveau Sujet
Exercice repère cylindrique
Bonjour tout le monde,
J'ai du mal avec les projections de vecteur je crois car je bloque dès le début de l'exo. J'ai la correction de l'exo mais seulement les réponses sans le raisonnement et je n'arrive pas a trouver ces réponses.
Voila l'énoncé:
On se propose d'étudier le mouvement d'un point M appartenant à un cercle de centre C et de rayon R roulant sans glisser sur un axe horizontal noté Ox: On supposera que le mouvement du cercle s'effectue dans le plan xOy et que C a une vitesse constante égale à v.
1) Montrer que vecteur(OM) = R(
-sin)
+ R(1-cos)
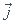et que la condition de roulement sans glissement de la roue se traduit par: vt=R
Mon début de réponse:
vecteur(OM) = vecteur(OI) + vecteur (IC) + vecteur(CM)
vecteur OI = R
vecteur IC = R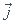
Je n'arrive pas a trouver vecteur CM pourriez m'indiquer comment faire svp
Edit Coll : une fois l'image suffit...
Salut lamat
Merci pour ta réponse j'ai compris. 
Dans la suite de l'exercice on calcule les vecteurs vitesse et accélération ainsi que leurs modules.
Puis on me demande de trouver le rayon de courbure. Dans ma correction ils écrivent:
vecteur(a) = vecteur(aT) + vecteur(aN
avec vecteur(aT) = (dv/dt) 
vecteur(T) accélération tangentielle
vecteur(aN) = v²/Rc vecteur(N) accélération normale avc Rc rayon de courbure
Pourrais-tu me dire d'où viennent ces égalités stp je ne vois vraiment pas.
je change l'exo pour expliqué les accélérations
on prend en référentiel l'axe fixe autour duquel tourne la roue:
vitesse linéaire v d'un point M de la roue = vitesse rotation de la roue W * distance entre M et le centre la roue.
le vecteur vitesse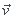 
= norme de la vitesse v * vecteur tangentiel T
quand on dérive le vect vitesse, c'est comme quand on dérive un produit de focntion en maths
(fg)'=f'g*fg'
il faut savoir que dvectT/dt= W*produit vectoriel(vectT,
)=W*vectN
d'où
d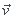/dt=dv/dt*vectT+v*dvectT/dt= dv/dt*T+v*W*vectT
Annuler
connectez vous