Bonjour j'ai un exercice à rendre pour mardi et cela fait plusieurs jours que je bloque sur la deuxième question.
Voici l'énoncé:
Une roue de rayon R (présentée sur la figure) roule sur l'horizontale (Ox), son centre C est animé d'un vecteur vitesse constant 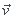_c.
La vitesse angulaire constante de rotation de la roue est notée =d/dt
Le repère (O;e_x;e_y)est lié au référentiel R du support plan et l'étude est effectuée dans le plan (Oxz)

1- A l'instant initial t=0, M est au point O.
La roue roule sans glisser sur son support et la vitesse de C vérifie la condition v_c=dx_c/dt=R.
Justifier succinctement cette égalité.

2- La roue démarre à l'instant initial t=0 avec une vitesse nulle. donnez les expressions des coordonnées x et z du point M en fonction de R, et du temps t.

3- Déterminez à partir de ces coordonnées les composantes du vecteur vitesse 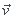(M)_/R et les composantes du vecteurs accélération a(M)_/R.

4- Montrez que le vecteur 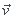(M)_/R est à tout instant orthogonal au vecteur IM.

5- Déterminez 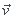(M)_/Ret a(M)_/R lorsque le point M est en contact avec le sol.

Pour la 1ère question j'ai dit qu'en se plaçant en coordonnées cylindriques on avait 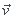(C)_/R=dR/dte_r+Red/dt+dz/dte_z
J'ai ajouter que R et z constants donc dR/dt=0 et dz/dt=0
On a donc v_c=Rd/dt=R

Pour la deuxième question je bloque. J'ai essayé d'utiliser la 1ère question mais sans réussite. De plus d'autres questions dépendent de celle-là.
Si vous pourriez me donner une piste, cela fait trois jours que je bloque.

Merci de votre aide.
Christophe