Inscription / Connexion Nouveau Sujet
Oscillations d'un pendule simple
Bonsoir !
Voilà j'ai un problème sur ce sujet . Je voudrais vous préciser ma situation cela fait un petit moment que je n'ai plus fait de physique (ayant eu une interruption dans mes études) et j'essai de tenter le CAPES de physique chimie .
Voici l'énoncé:
Un objet ponctuel A de masse m est suspendu à l'extrémité d'un fil de masse m négligeable et de longueur L don l'autre extrémité O es fixe. On ne considère pas les mouvements en dehors d'un plan vertical Ox perpendiculaire à un axe Oz horizontal. On repère A par l'angle  entre le fil et la vertical. On suppose que le référentiel terrestre est galiléen . On tient compte d'une force de frottements fluide proportionnel à la vitesse v. On note h le coefficient de proportionnalité
entre le fil et la vertical. On suppose que le référentiel terrestre est galiléen . On tient compte d'une force de frottements fluide proportionnel à la vitesse v. On note h le coefficient de proportionnalité
1) Déterminer l'équation différentiel du mouvement de A en appliquant le théorème de l'énergie cinétique
2) Les forces de frottements sont assez faibles pour que le régime soit pseudo périodique. Donner la condition sur h pour qu'il en soit ainsi.
3) On lâche le pendule sans vitesse initiale d'une position faisan un angle  0 faible . Linéariser l'equa diff du mvt puis déterminer l'expression de
0 faible . Linéariser l'equa diff du mvt puis déterminer l'expression de  en fonction de t
en fonction de t
4) Donner l'allure de la courbe représentant  en fonction du tps.
en fonction du tps.
Je pense que si j'arrive à répondre à la 1) le reste viendra tout seule
je sais qu'il a le travail qui intervient, que les forces qui s'appliquent sont le poids, la tension de fil et la force de frottement
Apres je suis bloquée
Si vous pouviez m'aidez au plus vite ce serai tres gentil !!


Bonjour !
Rien ne vaut un petit dessin pour y voir plus clair en mécanique, donc j'en ajoute un ici !
Comme tu l'as compris, il faut calculer le travail. Ici à mon avis, la seule force est la force gravitationnelle, .
Le travail infinitésimal avec du le vecteur unitaire représentant le chemin parcouru par le pendule. C'est là que l'on a besoin d'un petit schéma :
Avec le dessin, on peut voir que
Normalement à partir de cela tu peux continuer (il faut utiliser une formule de trigonométrie, puis intégrer sur tout le chemin parcouru). N'hésite pas à reposer des questions en cas de problème, et bon courage !
Merci Zofia de prendre de ton temps pour me répondre !
Mais justement il n'y a pas que ça comme force il y a également des forces de frottements et je ne sais pas comment sont elles représentées dans le schéma ?
De plus je crois qu'il y a la force de tension du fil non??
J'ai compris certaine chose en regardant dans des livres mais je ne sais pas si elles sont justes:
dEc=dw (R) R étant la résultante des forces Théorème de l'énergie cinétique
Ec énergie cinétique
dEc=dW(P)+dW(T)+dW(F) F force de frottement
Et dW(P)=-dEp si le poids est une force conservatrice.
Donc on peut écrire dEc+dEp=dW(F)
Sur P ,T et F il y a des flèches mais je ne sais pas comment faire sur ce site
Ep=mgLcos EC=1/2 mV[sup][/sup]
EC=1/2 mV[sup][/sup]
Maintenant je ne sais pas que vaut dW(F) ? Sachant F est une force non conservatrice
milles excuses, j'ai oublié les autres forces (tension du fil et forces de frottement). J'avais mal lu votre message en plus !
Mais je pense que vous pouvez exprimer le travail de ces forces de la même manière, en introduisant la variable à chaque fois. Ensuite, il faut exprimer l'énergie cinétique en différents points A et B ; la différence d'énergie cinétique est égale à la somme des travaux des forces (intégrés sur le chemin AB).
Pour une force non conservatrice, en effet on ne peut pas utiliser l'énergie potentielle. Il faut s'en tenir à la définition de dW.
Pour la tension du fil, je suppose qu'on la prend constante ?
Pour les forces de frottement, elles sont généralement proportionnelles à la vitesse.
Pour l'intégration on intègre en mais r est constant si on prend un référentiel dont l'origine est le point d'attache...
Sinon pour faire des flèches il faut utiliser les balises LTX (pour latex), et écrire \vec{F} entre les balises.
Merci
Pour la tension du fil , c'est une force perpendiculaire au sens de déplacement donc le travail s'annule
Ensuite j'ai également vu que v=l*d( )/dt Soit v=l
)/dt Soit v=l
 vitesse angulaire
vitesse angulaire
Est ce que je peux l'utiliser ici ?
Et autre question zofia (ou une autre personne qui peut me répondre  )
)
Si je m'en tiens à la définition de dW pour exprimer dw(F)
J'ai trouvé cette formule dW(F)=F*V(m) dt
F et V en vecteur
Et j'obtiens donc sans vecteur dW(F)=h*V^2
(Car F est proportionnel à la vitesse et j'appelle ce coef h
Puis je remplace par ce que j'ai dit tout à l'heure (enfin si c'est bon ?!) c'est à dire et j'obtiens dW(F)=2*h*l^2* '*
'* ''
''
Est ce que , ce que je raconte est juste ou pas du tout ? !

comme l'a dit zofia, il faut avant tout faire un dessin, en précisant bien les orientations (voir plus bas)
A est soumis à 3 forces: la tension du fil, le poids, la force de frottement
on peut écrire pour tout déplacement infinitésimal de A:
dEc =  W(P) +
W(P) +  W(f) (car T ne travaille pas pour la raison que tu as indiquée)
W(f) (car T ne travaille pas pour la raison que tu as indiquée)
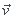 (A) = LO'
(A) = LO' 
Ec = 0.5mL2O'2
donc
dEc/dt = mL2O'O"
dEc = mL2O"dO
 W(P) = - dEp (je te laisse calculer Ep=Ep(
W(P) = - dEp (je te laisse calculer Ep=Ep( ) et dEp)
) et dEp)
pour un déplacement infinitésimal de A: LdO 
on a par ailleurs
 W(f) = -h
W(f) = -h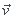 .LdO
.LdO  = -hL2O'dO (car f et
= -hL2O'dO (car f et 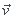 sont colinéaires)
sont colinéaires)
sauf erreur

Merci pour tes explication krinn
Mais il y a encore quelque chose que je n'ai pas compris
C'est ton expression de  W(f)
W(f)
Je ne comprend pas d'où vient LdO
Et est ce que l'on peut écrire O'dO=O"
Oui bien les deux dérives ne sont pas les mêmes ?
LdO est le déplacement élémentaire de A selon  (pour une variation de dO)
(pour une variation de dO)
O'dO=O"
non, car à gauche c'est un infiniment petit alors que O" est une quantité finie
Je trouve cette expression
Est que c'est ça?
 ''+(g/L)sin
''+(g/L)sin +(h/m)d
+(h/m)d =0
=0
Est ce normal que j'ai encore d ou il aurai du se simplifier?
ou il aurai du se simplifier?
c'est presque ça:
dEc = mL2O"dO
 W(P) = -mgLsinO dO
W(P) = -mgLsinO dO
 W(f) = -hL2O'dO
W(f) = -hL2O'dO
finalement: (O" +h/mO' +g/LsinO).dO = 0 pour tout dO
càd
O" + h/mO' + g/LsinO = 0
En fait je suis bloqué pour la suite de l'exercice lorsque l'on demande la condition sur h pour avoir un régime pseudo périodique
j'ai vu sur le net que si frottements sont faibles on a 2 alfa inferieur strictement à  0
0
avec  0=
0= (h/m)
(h/m)
Mais je vois pas le lien avec ce que j'ai trouvé
Pouvez vous m'éclairer je suis PERDU !
J'ai oublier de rajouter un point d'interrogation à la fin de mon dernier message
Ensuite pour lineariser l'équation différentiel j'ai trouvé que la forme générale de ce genre d'équation était
A'cos(  t)+B sin(
t)+B sin( t)
t)
Mais comment linéariser ceci ?
Merci Merci pour le temps que tu m'accordes à me répondre cela m'est d'une très grande aide
attention, la solution que tu indiques est celle de l'oscillateur harmonique (càd NON amorti)
ici on a une oscillation amortie (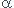 > 0) et un régime pseudo-périodique (
> 0) et un régime pseudo-périodique (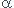 <1)
<1)
donc je te renvoie à ton cours pour trouver la forme générale de la solution de l'équa. diff.
O" + 2 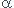 wo O' + wo2 O = 0
wo O' + wo2 O = 0
pour 0<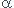 <1
<1
Je n'ai pas fait de cours à prtoprement parlé sur cette leçon donc je me renseigne sur ce que je trouve sur le net
Mais on est jamais trop sur et pour la forme generale cest
e−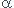 t(Acos
t(Acos t + B sin
t + B sin t)
t)

 O
O
 )
)

