Niveau terminale

Probleme sur Pendule élastique oblique

Posté par
kabrice 24-02-12 à 18:30

Bonsoir, svp j'ai des problemes sur cet exercice et j'ai grand besoin de votre aide.
Exo:
Deux ressorts (R) et (R') sont disposés suivant la ligne de plus grande pente x'x d'un plan incliné de 30° sur l'horizontale, comme l'indique la figure ci-contre. Les butées A et B sont distantes de L=0.80m. Les ressorts ont des spires non jointives, une masse négligeable, une longueur à vide l₀=0,25m et une constante de raideur k=10N/m.
1. On accroche à l'extrémité du ressort (R) un solide S assimilable à un point matériel de masse m=40g.
1.1. Calculer la longueur le du ressort à l'équilibre?
1.2. On écarte alors S de sa position d'équilibre d'une distance a= 4cm dans la direction x'x et on l'abandonne sans vitesse initiale. Déterminer la nature du mouvement de S. Calculer sa période.
2. S se décroche à un instant où l'allongement du ressort R est maximal. Le solide S glisse alors sur un plan incliné et va comprimer le ressort R'.
Soit d la variation maximale de longueur que subit le ressort (R').
Calculer d en considérant le système: S-Terre-ressort(R') et en utilisant la loi de conservation de l'énergie mécanique de ce système entre l'instant où S se décroche et celui où R' est en compression maximale.
On donne g=10m/s2
Merci de m'aider sinon j'ai surtout des problemes à la dernière question
Cordialement

Probleme sur Pendule élastique oblique

Posté par re : Probleme sur Pendule élastique oblique 24-02-12 à 19:32

Bonjour
Qu'as-tu fait dans cet exo ?...
La 1.1, je suppose...
La 1.2 ?

Posté par re : Probleme sur Pendule élastique oblique 24-02-12 à 20:36

Voici ce que j'ai fais:
1.1 A l'équilibre :(forces extérieurs)=0(vecteur nul)
cad P+R+T=0 (le tout en vecteur) cad Psin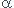-k(l_e-l₀)=0 ie le=((mgsin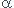+kl₀)/k), AN: le=0.27m
1.2. Ici, (forces extérieurs)=0(vecteur nul) cad P+R+T=0 (le tout en vecteur) cad mgsin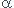-k(le+x-l0)=m(d²x/dt)
cad mgsin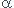-k(le-l0)-kx=m(d²x/dt)
Donc (d²x/dt)+(k/m)x=0
Ceci est analogue à l'équation différentielle (d²x/dt)+²x=0 qui est l'équation des mvts rectilignes sinusoïdales.
Conclusion: le mvt est un mvt rectiligne sinusoïdale de période T₀=2(m/k), AN: T₀=0.4s.
2. J'ai étais bloqué

Posté par re : Probleme sur Pendule élastique oblique 24-02-12 à 23:42

C'est pas mal !...

Citation :
cad mgsin

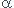-k(le-l0)-kx = m(d²x/dt²)
Donc (d²x/dt²)+(k/m)x = 0

C'est un peu rapide :
$\frac{d^2x}{dt^2}\,+\,\frac{k}{m}x\,=\,g\,sin\alpha\,-\,\frac{k}{m}(l_e-l_0)$
On peut chercher la solution générale de l'équation différentielle :
$\frac{d^2x}{dt^2}\,+\,\frac{k}{m}x\,=\,0$
qui est de la forme : $\frac{d^2x}{dt^2}\,+\,\omega^2x\,=\,0$
dont la solution est de la forme : $x\,=\,A\,cos\omega t\,+\,B\,sin\omega t$
Mais on peut calculer la solution totale en tenant compte du second membre. Je ne sais pas si tu sais le faire et ce n'est pas demandé explicitement.
Pour la 2, le solide S se détache quand le ressort est à l'élongation maximale. La vitesse est nulle. Donc le solide S descend le plan incliné en partant avec une vitesse nulle.
Il acquiert une certaine vitesse v (calculable) lorsqu'il atteint le ressort R'. Il a donc une certaine énergie cinétique. L'énergie mécanique totale du solide S est transformée en énergie dans le ressort par compression de celui-ci ( $\frac{1}{2}kd^2$ ) d'où la calcul de d.

Posté par re : Probleme sur Pendule élastique oblique 25-02-12 à 06:15

Bonjour, j'ai 2 préoccupations:
L'équation différentiel du mvt est (d²x/dt²)+(k/m)x=gsin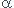-(k/m)(l_e-l₀) ou simplement (d²x/dt²)+(k/m)x=0 ?. Je ne comprends pas bien ?.
Et pour la dernière question, (0.5kd²) est réelement égale à quoi ?. En effet, je ne comprends pas bien l'explication de la dernière question, je ne comprends pas où vous voulez en venir ?
Merci

Posté par re : Probleme sur Pendule élastique oblique 26-02-12 à 22:48

De toute évidence, l'équation est :
$\frac{d^2x}{dt^2}\,+\,\frac{k}{m}x\,=\,g\,sin\alpha\,-\,\frac{k}{m}(l_e-l_0)$
La solution totale est la solution générale c'est-à-dire la solution de l'équation sans second membre :
$\frac{d^2x}{dt^2}\,+\,\frac{k}{m}x\,=\,0$
à laquelle on ajoute une solution particulière due au second membre.
Mais, pour déterminer la nature du mouvement de S, la solution générale peut suffire.
$\frac{1}{2}kx^2$ est l'énergie potentielle d'un ressort allongé ou comprimé de la longueur x.
Donc, ici, toute l'énergie du solide S est transformée en énergie potentielle dans le ressort lors de la compression de celui-ci...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Probleme sur Pendule élastique oblique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique