Bonjour à tous , voila j'ai un problème d'exercice , c'est la fameuse histoire du skieur qui descend une pente. Voici l'énoncé :
Un skieur se trouve au sommet d'une piste faisant un angle 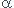avec l'horizontale et de dénivelée h. A t=0, il part sans vitesse initiale.

Toute la suite de l'exercice se résoudra par l'approche énergétique !

L'exercice se compose de 2 partie , sans et avec frottement :
- J'ai réussi sans problème la partie sans frottement , on avait que 2 forces : le poids (force conservative) et la réaction du support (le travail est nul car perpendiculaire au mouvement)

J'ai trouvé une vitesse de v = (2gh) ainsi qu'une conversion parfaite entre l'énergie cinétique et l'énergie potentielle.


- Maintenant, passons avec les frottements fluide, j'expose ma méthode : (les vecteurs sont représentés ici par des '_')

Enoncé : Etude avec un frottement solide de coefficient f.

"Considérons l'objet ponctuel dans le référentiel lié à la Terre, supposé galiléen"

Inconnues cinématique : x(t)
Bilan des forces :
P = m'g' (force conserv)
N = N'uz' (force non conserv + ne travaille pas)
F = -f'v' (opposé au mouvement)

(Schéma tout en bas)
Em = (force non conservative) = 0
Em(t) = Em(t=O) = constante

Em(A) = (1/2)mv_A² + mgh
or au point A , v = 0 donc
Em(A) = mgh

Em(B) = (1/2)mv_B² + mgh
or au point B , h=0 donc
Em(b) = (1/2)mv_B²

Mais la je ne vois pas où introduire la force de frottement vu que ce n'est pas une force conservative , me suis-je trompé sur Em(A) et Em(B)

Sinon à la question 2.) Il me demande de calculer le travail de la force de frottement solide lors du déplacement...

J'espère avoir été clair et j'attend avec impatience vos réponses Bonne soirée!